虹润温控表在恒温箱控制中的应用
摘 要:在周围环境温度不同的情况下,通过实验的方法得出了3个恒温箱的数学模型。针对恒温箱这个时变的系统,建立了一个可以对恒温箱实现高精度控制的控制算法数学模型,并应用在所建立的3个恒温箱模型中。该控制器不仅保持了常规PID控制器的优点,而且具有很强的鲁棒性和适应性。仿真结果表明系统可以达到很好的动静态性能指标。
关键词:恒温箱温度控制 模糊 PID 控制
引言
目前常用的恒温箱可分为3类:高温恒温箱,箱温大于60℃;中温恒温箱,箱温在-10~60℃;低温恒温箱,箱温小于-10℃。本人自己研制了一新型的恒温箱系统,要求恒温箱内温度能精确控制在25℃。由于外界环境的温度可比25℃高也可低,因此恒温箱具有制冷系统和加热系统,所设计恒温箱系统由恒温箱箱体、齿轮泵、压缩机系统、电加热管、油管以及控制器等组成。温度控制系统在箱体外部对流经油管的变压器油控温,经过控温的变压器油重新流回恒温箱的箱体内。因为恒温箱在冬天和夏天,所处的环境温度不同,所以恒温箱的温度模型也是不同的,也可以说恒温箱是个时变的系统。通过实验测试的方法测量出恒温箱在外界环境温度为8℃,15℃和35℃时系统在电加热情况下的模型分别为

本文就是要针对所建立的数学模型设计一个可以对恒温箱实现高精度控制的控制算法。
1 模糊PID 控制原理
模糊理论是在美国柏克莱加州大学电气工程系Lotfi. A. Zadeh 教授于1965 年创立的模糊集合理论的数学基础上发展起来的,他提出了能够表征人类思维中模糊概念的方式——隶属度函数,发表了题为“Fuzzy Set"的论文[1]。模糊控制器FC (fuzzy controller)也称为模糊逻辑控制器FLC (fuzzy logic controller)[2~4]。模糊PID 控制器是一种在常规PID 调节器的基础上,应用模糊集合理论根据控制偏差、偏差绝对值,在线自动整定比例系数、积分系数和微分系数的模糊控制器。模糊逻辑控制器动态性能抗扰性和PID 控制器稳态精度高,取两者的优点就构成模糊PID 控制器。其控制器不仅保持了常规PID控制器的优点,而且具有很强的鲁棒性和适应性。自适应模糊PID 控制器以偏差e 和偏差变化率ec 作为输入,可以满足不同时刻偏差e 和偏差变化率ec 对PID 参数自整定的要求。利用模糊控制规则在线对PID 参数进行修改,便构成了自适应模糊PID 控制器,其结构如图1 所示。
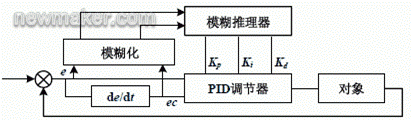
图1 自适应模糊PID控制器
PID 参数自整定的实现思想是先找出PID 的3 个参数与偏差e 和偏差变化率ec 之间的模糊关系,在运行中通过不断检测偏差e 和偏差变化率ec ,再根据模糊控制原理来对3 个参数进行在线修改,以满足不同e 和ec 对控制参数的不同要求,而使被控对象有良好的动、静态性能。
2 模糊PID 设计
2.1 控制器结构设计
此处的模糊PID 控制器采用恒温箱内的温度偏差e 和偏差变化率ec 作为输入变量[5],以 ΔKp 、 ΔKi 和 ΔKd作为输出。模糊集E 及模糊集EC 均取为,论域为[-3,3];模糊输出 ΔKp 取为,论域为[-0.3,0.3]; ΔKi 取为,论域为[-0.6,0.6];ΔKd 取为,论域为[-3,3];E 、EC 、 ΔKp 、 ΔKi 和 ΔKd 的隶属函数曲线分别如图2 所示。
图2 隶属函数2.2 控制规则
PID 参数的整定必须考虑到在不同时刻3 个参数的作用以及相互的互联关系。根据 Kp 、 Ki 和 Kd 对系统输出特性的影响情况,可归纳出在一般情况下,在不同的|e|和|ec|时,被控过程对参数 Kp , Ki 和 Kd 的自整定要求如下:
① 当 |e| 较大时,为加快系统响应速度并防止起始偏差e 瞬间变大,可能引起微分过饱和,而使控制作用超出许可范围,应取较大的 Kp 和较小的 Kd ,同时为避免系统因积分饱和所引起的较大超调,应对积分作用加以限制,通常取Ki =0 ;
② 当 |e| 和|ec| 为中等大小时,为使系统响应的超调减小,并保证系统的响应速度, Kp 、 Ki 、 Kd 的值的大小适中;
③ 当 |e| 较小时,为使系统具有良好的稳态性能,应增加 Kd 和 Ki 的值,同时为了避免系统在设定值附近振荡,并考虑系统的干扰性能,应适当地选取 Kd 的值,其原则是:当|ec| 较小时, Kd 可取的大些,通常取为中等大小;当|ec| 较大时, Kd 应取小些。
根据以上经验,本文所采用的模糊控制规则表如表1所示。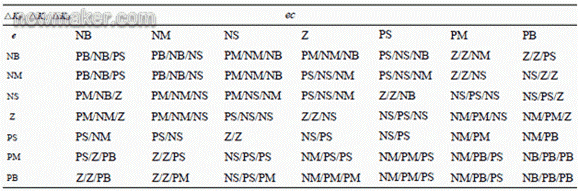
表1 模糊控制规则表
2.3 泄漏检测流程
在本控制器中采用如下的推理形式:
R1 :如果e 是 A1 , ec 是 B1 ,则 Kp 是 CP1 , KI 是 CI1 , KD 是CD1
本控制器中,模糊推理采用最大最小合成法,模糊量的清晰法采用最大隶属度方法,该方法是选择模糊子集中隶属度最大的元素称为控制量。若对应的模糊决策的模糊集为c ,则决策(所确定的精量确量) u∗ 应满足
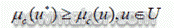
得出 PID 的各个调整参数后,就可以实现模糊PID 的参数调整算式如下:
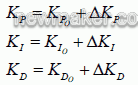
式中: KPO 、 KIO 、 KD0 为初始值; ΔKP 、 ΔKI 和 ΔKD 为经模糊推理后得到的PID的调整参数值。
3 控制算法仿真研究
按照上面所介绍的模糊PID,将此方面控制到上面所采用的3 个模型,这时PID 的3 个参数的初始值分别取为 KP0 =0.9、 KI0 =0.000 85、 KD0 =1.0。此时的仿真曲线如图3 所示。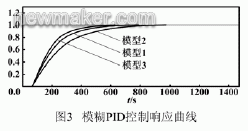
对于不同模型的控制性能指标如表2 所示。
表2 系统性能指标
从图中可以看出,模糊PID 控制的控制效果很明显。其结合了传统的PID 控制的性能稳定,可以消除稳态误差的特点。同时,也具有模糊控制的不依赖于数学模型,动态性能好的特点。从表2 可以看出控制系统在时间1 200 s 就已经进入了稳定状态。其系统稳态误差为0.001,满足系统要求的在时间1800s 时,系统的稳态误差为0.002 的要求。从这3个模型的仿真的可以看出模糊PID 控制对于时变的、纯滞后的、非线性的一阶大惯性的系统可以取得很好的效果。
4 结束语
通过仿真实验可以看出,所设计的模糊PID 控制对于所建立的3 个数学模型都可以达到很高的动静态性能指标,所设计的模糊控制器对于所研制的恒温箱可以达到高精度的控制。



